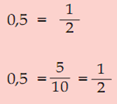Asyiknya Belajar Pecahan
Rabu, 13 Februari 2013
Pengertian bilangan pecahan
BAGIAN PECAHAN PECAHAN
A. Pengertian Pecahan
- Bilangan pecahan merupakan bilangan yang mempunyai jumlah kurang atau lebih dari utuh .
- Terdiri dari pembilang dan penyebut .
- Pembilang merupakan bilangan terbagi
- penyebut merupakan bilangan pembagi
B. Pecahan Senilai
Penengertian dari pecahan senilai dapat kita gambarkan dengan cerita berikut ini.
Ibu Linda membuat sebuah puding yang besar, sebagian puding tersebut kemudian dipotong dan dibagikan kepada semua anggota keluarganya yang terdiri atas empat orang. 1/8 bagian diberikan kepada Linda, 1/8 bagian yang lain diberikan kepada Lusi, adik Linda, ayah dan ibu Linda juga masing-masing mendapat 1/8 bagian.
Sisa puding yang belum dipotong, seperti yang terlihat pada gambar di atas, tinggal 1/2 bagian dari besar puding mula-mula.
Dapat kalian lihat pada gambar di atas, jika semua puding yang sudah dipotong disatukan, besarnya sama dengan sisa puding yang belum dipotong.
1/2 dan 4/8 dapat disebut sebagai pecahan yang senilai karena meskipun lambang bilangannya berbeda, kedua pecahan tersebut nilainya sama.
Beberapa contoh pecahan lain yang senilai adalah :
selain 2/4 dan 4/8 masih banyak pecahan lain yang senilai dengan 1/2, diantaranya 5/10, 6/12, 7/14, dst.
Kita dapat membuat pecahan yang senilai dengan pecahan tertentu dengan cara mengalikan atau membagi pembilang dan penyebut pecahan tersebut dengan bilangan yang sama. Contoh:
A. Pengertian Pecahan
- Bilangan pecahan merupakan bilangan yang mempunyai jumlah kurang atau lebih dari utuh .
- Terdiri dari pembilang dan penyebut .
- Pembilang merupakan bilangan terbagi
- penyebut merupakan bilangan pembagi
B. Pecahan Senilai
Penengertian dari pecahan senilai dapat kita gambarkan dengan cerita berikut ini.
Ibu Linda membuat sebuah puding yang besar, sebagian puding tersebut kemudian dipotong dan dibagikan kepada semua anggota keluarganya yang terdiri atas empat orang. 1/8 bagian diberikan kepada Linda, 1/8 bagian yang lain diberikan kepada Lusi, adik Linda, ayah dan ibu Linda juga masing-masing mendapat 1/8 bagian.
Sisa puding yang belum dipotong, seperti yang terlihat pada gambar di atas, tinggal 1/2 bagian dari besar puding mula-mula.
Dapat kalian lihat pada gambar di atas, jika semua puding yang sudah dipotong disatukan, besarnya sama dengan sisa puding yang belum dipotong.
1/2 = 4/8
1/2 dan 4/8 dapat disebut sebagai pecahan yang senilai karena meskipun lambang bilangannya berbeda, kedua pecahan tersebut nilainya sama.
Beberapa contoh pecahan lain yang senilai adalah :
selain 2/4 dan 4/8 masih banyak pecahan lain yang senilai dengan 1/2, diantaranya 5/10, 6/12, 7/14, dst.
Kita dapat membuat pecahan yang senilai dengan pecahan tertentu dengan cara mengalikan atau membagi pembilang dan penyebut pecahan tersebut dengan bilangan yang sama. Contoh:
3 = 3 x 2 = 6
4 4 x 2 12
C. Menyerdehanakan pecahan
Pecahan dapat disederhanakan dengan mencari FPB dari pembilang dan penyebutnya. Agar kamu lebih memahaminya, perhatikan contoh berikut.
kita juga dapat memakai cara lain,dengan cara berikut ini :
Mengubah pecahan campuran menjadi pecahan biasa terlebih dulu, kemudian disederhanakan.
D. Hubungan Antar Jumlah Bilangan
Perbandingan Bentuk - Bentuk Pecahan
5. | Mengubah Pecahan Ke dalam Bentuk Desimal dan Sebaliknya | |||||||||||||||||
|
Bilangan desimal 0,5 sama dengan pecahan untuk menyederhanakan pecahan 5/10, maka penghitung dan penyebut dibagi dengan bilangan yang sama (jumlah terbesar yang dapat membagi keduanya) yaitu jumlah 5, sehingga penghitung (5: 5 = 1) dan penyebut (10: 5 = 2). Jadi 0,5 = 1/2
| 6. | Mengubah Desimal Ke dalam Bentuk Persen dan Sebaliknya | ||||||||||||
|
Langganan:
Komentar (Atom)