B.
| PERBANDINGAN DAN BENTUK - BENTUK PECAHAN
| 1. | Pecahan dalam Perbandingan |
| Sebuah pecahan yang menunjukkan rasio tidak sama dengan pecahan yang mewakili bagian dari keseluruhan (utuh). Kapan pecahan biasa digunakan untuk menunjukkan rasio akan memiliki interpretasi yang berbeda dibandingkan pecahan sebagai bagian yang utuh. Misalnya: penghitung dari sebuah pecahan sebagai rasio mungkin menyatakan jumlah obyek dalam kelompok obyek.Contoh: Dinda dan Dita membagi tanggung jawab mengelola toko kelontong. Dinda dalam 1 minggu menjaga toko selama 4 hari, sedangkan Dita 3 hari. Ketika Dinda telah menjaga toko selama 20 hari, berapa harikah Dita telah menjaga tokonya?
Jawab: Rasio untuk masalah di atas adalah 4: 3 (dibaca 4 dibanding 3). Sebuah pernyataan dapat digunakan untuk memecahkan masalah itu.
Perbandingan merupakan pernyataan bagian dari jumlah atau kelompok tertentu.Pernyataan perbandingan harus ditulis dengan pecahan yang sangat sederhana. Cara menyederhanakan perbandingan sama halnya dengan menyederhanakan pecahan, yaitu dibagi dengan bilangan yang sama. |
2. |
Skala |
| Skala, perbandingan, dan pecahan memiliki hubungan yang erat. Hal ini karena ketiganya memiliki simbol (tanda) yang sama, yaitu tanda untuk (:).Saat kita mengamati peta yang tergantung di dinding, atau pada atlas, di setiap sudut peta tersebut selalu tertulis kata skala yang disertai angka yang merupakan perbandingan. Misalnya, skala 1: 2.000.000, 1: 2.500.000, 1: 200, 1: 100, dan seterusnya.Skala banyak digunakan dalam atlas maupun dalam menggambars esuatu yang bentuk aslinya berukuran besar seperti lapangan atau bangunan.Skala biasanya diatur dalam ukuran cm hingga 1 cm pada peta dikalikan pada skala yang telah ditetapkan. Misalnya skala 1: 2.500.000, sehingga 1 cm menjadi 1 x 2.500.000 = 2.500.000 cm saat dijadikan ukuran dalam km menjadi 2.500.000: 100.000 = 25 km. Jadi, setiap 1 cm pada peta berjarak 25 km jarak yang sebenarnyaPerhatikan penggunaan skala berikut ini! Pada sebuah atlas tertera skala 1: 2.000.000. Setelah diukur, jarak dari kota A ke kota B sepanjang 4 cm. Berapa kilometer jarak sebenarnya dari kota A ke kota B?Jawab: Jarak sebenarnya adalah 4 x 2.000.000 = 8.000.000 cm. Dari cm menjadi km adalah dengan cara membagi 100.000 sampai 8.000.000: 100.000 menjadi 80 km. |
3. MENGUBAH PECAHAN BIASA MENJADI PECAHAN CAMPURAN
Contoh:
- Ubahlah
 ke dalam bentuk pecahan campuran! ke dalam bentuk pecahan campuran!
- Ubahlah
 ke dalam bentuk pecahan campuran! ke dalam bentuk pecahan campuran!
4. MENGUBAH PECAHAN KE PERSEN DAN SEBALIKNYA SEBALIKNYA
|
|
| a. | Mengubah pecahan ke dalam bentuk persen |
| Cara mengubah pecahan biasa ke dalam bentuk persen, yaitu dengan cara mengubah penyebut pecahan tersebut menjadi 100, karena persen merupakan per seratus Pahamilah perubahan pecahan menjadi persen di bawah ini!
 | Karena penyebut pecahan (2) ingin jadi 100, maka penyebut harus dikalikan ke 50 (2 x 50 = 100), sehingga penghitung pun harus dikalikan dengan bilangan yang sama (1 ∞ 50) hingga 1/2 = 50% |
|
b. |
Mengubah persen ke bentuk pecahan biasa |
| Mengubah persen ke dalam bentuk pecahan biasa dilakukan dengan cara sebagai berikut.
1. Dari bentuk persen diubah dulu menjadi pecahan biasa (per seratus).
2. Taksir atau cari pembagi terbesar dari jumlah penghitung dan penyebut.
3. Untuk penghitung maupun penyebut dengan bilangan pembagi tersebut.
Contoh
 | Pembagi terbesar dari 75 dan 100 adalah 25, maka kedua bilangan 75 dan 100 (pembilangdan penyebut) dibagi oleh bilangan 25. Menjadi
75: 25 = 3 (penghitung)
100: 25 = 4 (penyebut) |
|
|




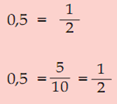


Tulisannya bagus. Sangat membantu dalam pengerjaan soal kuliah. Terima kasih. ^_^
BalasHapus